RADAR SIGNATURE MODELING OF A WALKING MAN

Ground radar systems used for border and perimeter surveillance are designed to detect moving vehicles and people. Modeling Doppler spectra for vehicles is straight forward; the problem is harder for moving humans. Here, I present the calculated velocity spectrum of a walking person displayed from four different canonical points of view. The raw data for this analysis comes from motion capture measurements of an actual human, so this represents real data, not an analytical model for the human gait. (A model of the human gait could be derived from these measurements, though.) Using an analysis technique based on my raytracing codes, the Doppler spectra for any type of activity can be modeled, e.g. running, jumping, climbing, etc. Modeling Doppler spectra for these activities would be cheaper and more convenient than setting up experiments with real radars. This model can be used as the basis for representing people of different heights and average walking velocities through simple linear scaling.

Doppler spectra modeling is not limited to radar instrumentation. Acoustic modeling can also be performed, e.g. for a sonogram of the beating heart. It's just a matter of having the dynamic model of the subject of interest.

Walking Man Movie

The movie in this panel shows a side by side comparison of a stick representation of a walking human next to the instantaneous representation of his Doppler spectrum. The displayed data covers approximately 0.5 seconds of time. The movie is played in an infinite loop to mimic continual walking.

Any computation of Doppler spectrum implies an orientation of the subject to the transmitter. For this example, the radar is assumed to illuminate the subject diametrically opposite the walking direction and parallel to the ground. The spectrum was calculated at 1.0mm/sec increments--too small to be resolved at these plotting scales. Further, the spectrum was coherently added over the extent of the subject representation in 1.0mm increments. Phase addition was performed for a wavelength appropriate to a K band radar. Other wavelengths could be chosen as the basis for propagation delay.

And a note about the stick representation of our human walker. For the radar/model orientation here, the stick model yields a precise velocity model and a fairly accurate amplitude estimation. However, when the radar is to the side, a stick model will not be as faithful to the amplitude estimates, primarily because of self-shadowing of body parts (arm by the torso, leg by another leg.) A fully polygonalized model should be used for this level of accuracy. Also polygonalized models should be used when modeling groups of people.

Depending on the capabilities of your computer and browser, the movie may not appear to depict a walker moving at a quick and steady pace. The original movie played with a dedicated media player, however, does show proper depiction of "smooth," walking motion.

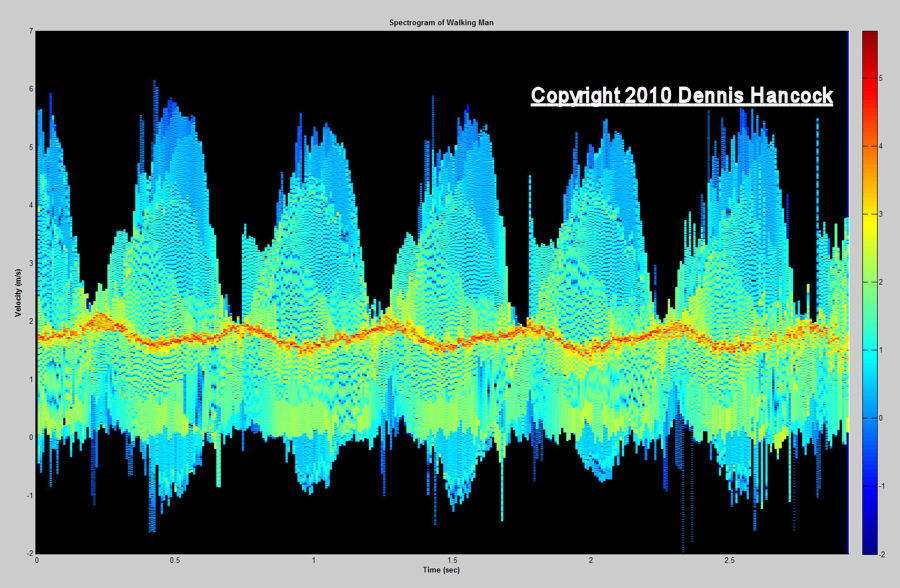
Walking Man Spectrogram (Spectrum Vs. Time)

Here, the same spectrum data is plotted vertically for each of the 351 time instants in the model for which motion data is available. The span of time represented here is 2.925 seconds.

Several features immediately stand out representing the radar signature this way. First, the entire extent of the human body does not move at a single velocity, but displays a range of velocities, both positive and negative, while moving generally towards an observation position. Second, the motion is approximately periodic with a 0.5 second interval. And third, there is an asymmetry in this person's velocities considering motions toward and away from the radar.

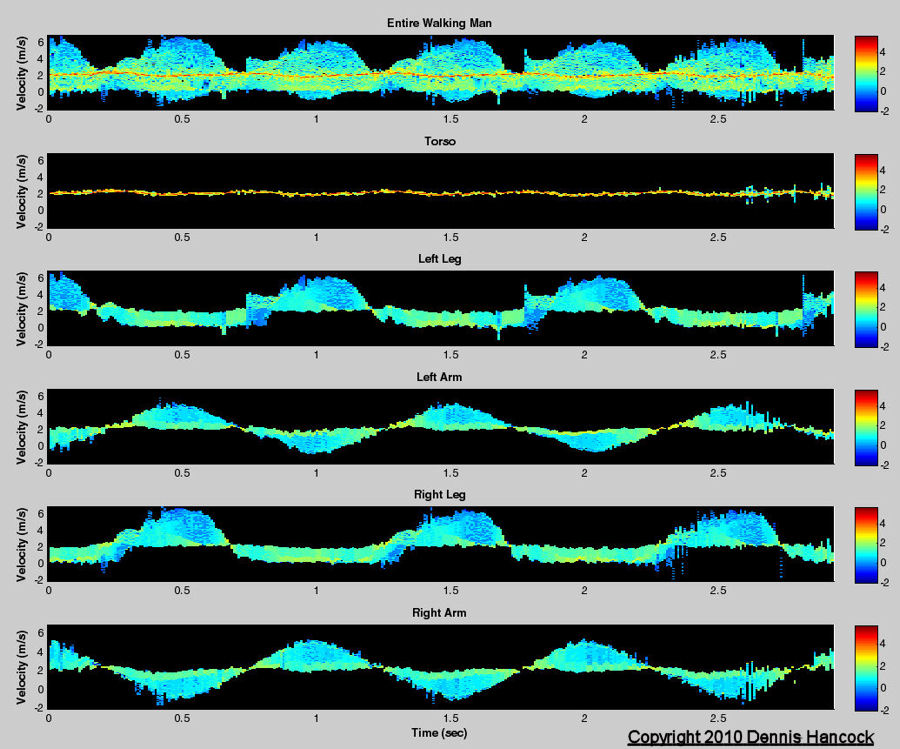
Walking Man Spectrum By Body Part Vs. Time

The human stick model is exposed by bone composition allowing for the interesting observations in this panel. Again the instantaneous spectrum is displayed as a function of time for the 351 frames spanning 2.925 seconds. However, for this plot the spectrum contributions by major body components are isolated for study.

It can be seen that the major component of reflected radar energy comes from the torso. Even the torso doesn't move at a single velocity, apparently slightly slowing/advancing when the feet touch the ground.

At this velocity the left-arm/right-leg and right-arm/left-leg can be thought of as swinging pendulums. The arm and leg of each pair swing in unison and phase. However, the arm/leg pairs move in opposite phases presumably for balancing reasons. The maximum instantaneous frequency bandwidth occurs when all arms and legs are at the human's side. The minimum instantaneous frequency bandwidth roughly occurs when the arms and legs are at the maximum extent of their swing when their velocities are zero.

The maximum frequency deviations come from the feet which is a consequence of their length being longer than the arms. Radar systems designers relying on these higher frequency components for detection purposes should be cognizant that these frequencies may not always be present due to terrain masking.

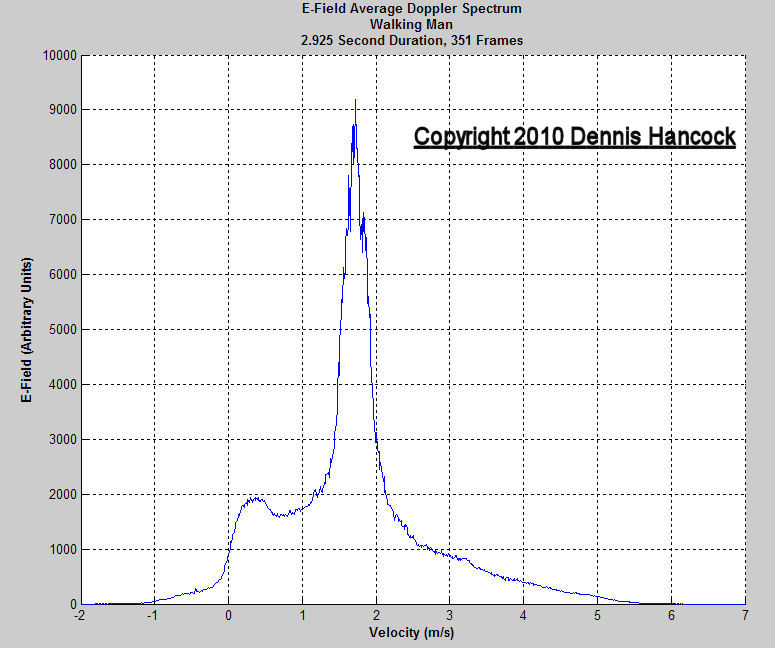
Walking Man Power Spectral Density

Finally, I de-emphasize the temporal content of the instantaneous spectrum and add the absolute values of each spectrum for presentation in this panel.

Two items of interest are exposed by this presentation modality. First, what is casually thought of as the walking velocity of a person is more strikingly revealed as approximately 1.7 m/sec. And second, there is the 0.5 m/sec bump feature centered at approximately 0.3 m/sec which may be an identifying signature for this person. It would be interesting to study this feature in detail.